Norm-Referenced Grading

In norm-referenced grading, the class sets the standard to which the individual will be compared. The students who get the highest total points at the end of the course will get A’s, even if they only successfully complete half of the learning objectives. Those with the least points fail.  In discussions of teaching and assessment this is often called grading on a curve.

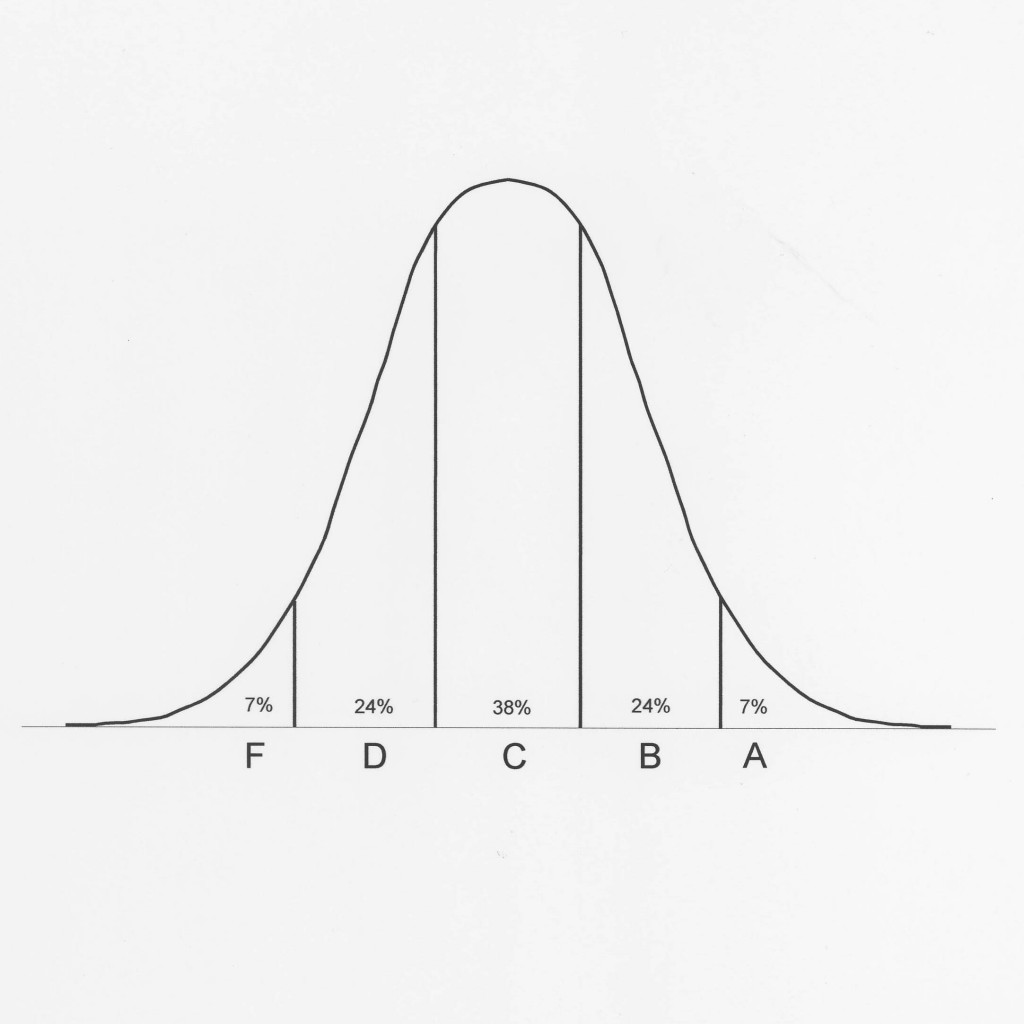
The number of students getting each letter grade is determined by what is referred to as a normal distribution (see Fig. 4). The reasoning behind this is that on any measure of individual differences, most of the scores will cluster around the mean. The number of scores below or above the mean will diminish with distance from it. So, on an imaginary test of 100 questions, where the average score is 50 right, we would expect to find a great many students getting 50 or 49 or 51. Very few will get either 5 right or 95 right. This is, of course, because a great many people are of average ability and motivation, or nearly so. Very few deviate substantially from the average.

Normal Curve with Possible Grade Distribution

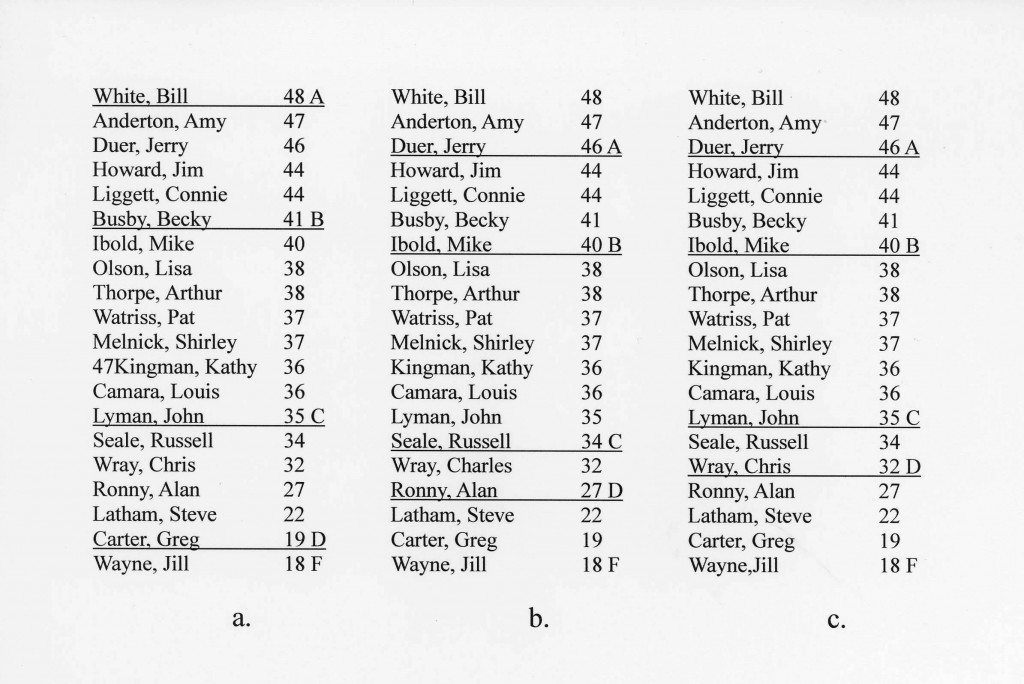
Using this curve as the rationale for distributing grades, you would give the top 7% of your students an A, the next 24% a B, and so on. Naturally, these percentages are arbitrary. You could just as well use 10%-20%-40%-20%-10%, or any other, for that matter. Grades are assigned after rank ordering the scores, such as in Figure 5a.

While this argument seems to suggest that you will usually get a normal distribution of scores on your tests, you almost certainly never will. Score distributions which fit the model in Normal Curve diagram above will only be found where there is a very large population of test-takers, perhaps thousands.

Assigning Letter Grades

In the above list, column a might be the result of grading based on a strict interpretation of the normal curve and the percentages for each letter grade.  But most teachers would likely consider this too severe.  Also, in a real class, you might be justifiably reluctant to apply the percentages of the normal distribution. Certainly, in a grouped class of high achievers, it would be absurd to feel obligated to assign D’s and F’s. Indeed, A’s and B’s with nothing lower could be reasonable. Even in an average class, you might be so encouraged by the performance of even the poorest students that you could choose to give no grade lower than a C. For this reason, most teachers will look at the rank order list of grades and assign grade boundaries where natural divisions seem to occur (see column b in the above list). While this technique may be more satisfying for the teacher, it is also more likely to be criticized by students just missing the cutoff.

If the teacher faithfully employs norm referenced grading, then the parents’ question about their child’s class standing is reliably answered. This type of grading also relieves the teacher of any concern about fairness in awarding grades. New teachers are especially concerned that students don’t score well on tests because the test was too hard. Norm-referenced grading factors out the difficulty of the test and any deficiencies in the instruction.

It does have serious problems, however. First, it pits one student against another. High scoring students displace others below them who may then receive lower grades. Also, the most capable students can get high grades with little work, while less able students may find it impossible to get good grades. Another problem is that norm-referenced grades don’t necessarily provide any indication of a student’s mastery of the learning objectives in the course. A student demonstrating competence on only half the objectives would nevertheless get an A if his was the highest score. Finally, with this grading approach, it is impossible for a student to project how he might do on future work, since the grades are determined by a constantly shifting frame of reference. It could be argued that that would encourage each student to work to the limit of his potential. Unfortunately, most students pick a lesser goal (perhaps a B or a C). For those, test grades too often come as a surprise.

Norm-referenced grading sends a questionable philosophical message to students as well. Since student performance determines the grading scale, the importance of your learning objectives is diminished. After all, if one can earn an A by knowing only a fraction of the material, many will reason that much of your course content wasn’t that important. Students won’t work to master the material, just each other. While competition might be a motivator for a class of high achievers, the average student will find mediocrity entirely adequate.

Go to “Criterion-Referenced Grading“